Зубчатые механизмы. Теория механизмов и машин. Курс лекций

Кинематика планетарных механизмов

Краткое содержание: Многозвенные зубчатые механизмы. Кинематика рядового зубчатого механизма. Кинематика ступенчатого механизма. Формула Виллиса для планетарных механизмов. Кинематическое исследование типовых планетарных механизмов графическим и аналитическим методами.

При проектировании зубчатых механизмов многих машин и приборов (манипуляторов, станков, автомобилей, летательных аппаратов, индикаторов, тахометров, печатающих устройств ЭВМ и др.) возникает необходимость обеспечить передачу вращения с большим передаточным отношением или при значительных межосевых расстояниях. В таких случаях применяют многозвенные зубчатые механизмы либо снижающие скорость вращения выходного вала по сравнению с входным - редукторы, либо повышающие ее - мультипликаторы.

Многозвенные зубчатые механизмы могут быть как плоскими, так и пространственными. Они подразделяются на два основных вида:

зубчатые механизмы с неподвижными осями всех колес;

зубчатые механизмы, оси отдельных колес которых перемещаются относительно стойки.

К первому виду механизмов относятся рядовые (с развернутой схемой) и ступенчатые зубчатые механизмы, подвижность таких механизмов

. Ко второму виду относятся планетарные , дифференциальные

, замкнутые дифференциальные и волновые зубчатые механизмы. Большим достоинством механизмов второго вида является их компактность. Проектирование многозвенных зубчатых механизмов включает два этапа: выбор структурной схемы; определение чисел зубьев для воспроизведения заданного передаточного отношения.

Общее передаточное отношение многозвенного механизма равно произведению передаточных отношений отдельных механизмов (ступеней), последовательно включенных в его состав

Кинематика рядового зубчатого механизма

Рядовым зубчатым механизмом называется сложный зубчатый механизм с неподвижными осями колес, образованный последовательным соединением нескольких пар единичных зубчатых колес. Имея схему передачи и числа зубьев или радиусы начальных окружностей колес можно определить общее передаточное отношение такого редуктора аналитически или графически. (Для колес без смещения, которые обычно используют в редукторах , начальные окружности совпадают с делительными; для колес со смещением -

Рассмотрим кинематику рядового механизма составленного из трех зубчатых передач внешнего зацепления. Схема механизма изображена на рис.

, где знак «+» соответствует внешнему зацеплению зубчатых колес, а знак «-» внутреннему.

Таким образом, для приведенного механизма получим:

На основе чего можно получить общую формулу для определения передаточного отношения рядового редуктора:

Общее передаточное отношение рядового зубчатого механизма постоянно и равно обратному отношению чисел зубьев или радиусов крайних колес. Знак передаточного отношения определяется множителем

, где - число передач внешнего зацепления.

Графическое определение передаточного отношения таких механизмов осуществляется методом планов скоростей (треугольников скоростей). Треугольник скоростей можно построить, если для звена известны линейные скорости не менее двух точек звена (по величине и направлению). Используя этот метод можно получить наглядное представление о характере изменения скоростей от одного вала колеса к другому, а также можно определить графически угловую скорость любого колеса.

,тогда

, где знак отношения определяется по знаку тангенса.

Передаточное отношение рядовых механизмов обычно не велико, так как оно ограничивается предельными размерами крайних колес (1,4), а числа зубьев промежуточных колес (2,3) не влияет на общую величину передаточного отношения. Применяют такие механизмы там, где необходимо изменить вращение ведомого вала, не изменяя при этом направление движения ведущего – коробки передач, либо при передаче движения на значительные расстояния, если нет возможности увеличить размеры ведущего и ведомого колес.

Кинематика ступенчатого зубчатого механизма

Рассмотрим кинематику ступенчатого механизма составленного из трех зубчатых передач: двух внешнего зацепления (1-2) и (3-4) и одной внутреннего зацепления(5-6). Схема механизма изображена на рис.

Аналитическое определение передаточного отношения

Аналитическое определение передаточного отношения основывается на формуле:

Аналитическое определение передаточного отношения.

Заданный планетарный механизм с двумя внешними зацеплениями зубчатых колес. Аналитическое определение передаточного отношения основывается на формуле:

так как колеса 2-3 находятся на одном валу, соответственно вращаются с одинаковой угловой скоростью.

Используя основную теорему Виллиса, для заданного обращенного механизма получим:

По формуле Виллиса

Графическое определение передаточного отношения .

,тогда

, где знак отношения определяется по знаку тангенса.

Кинематика ступенчатого зубчатого механизма

Аналитическое определение передаточного отношения

Аналитическое определение передаточного отношения основывается на формуле:

так как колеса 2-3 и 4-5 находятся на одном валу, соответственно вращаются с одинаковыми угловыми скоростями.

Используя основную теорему Виллиса, для заданного механизма получим:

На основе чего можно получить общую формулу для определения передаточного отношения ступенчатого редуктора:

Общее передаточное отношение ступенчатого зубчатого механизма равно отношению произведения чисел зубьев ведомых колес к произведению чисел зубьев ведущих колес. Знак передаточного отношения определяется множителем

, где- число передач внешнего зацепления.

Графическое определение передаточного отношения

Графическое определение передаточного отношения также осуществляется методом планов скоростей (треугольников скоростей).

где знак отношения определяется по знаку тангенса или по правилу стрелок.

За счет подбора чисел зубьев в ступенчатом механизме можно получить большие передаточные отношения при тех же габаритах, что у рядового.

Ступенчатые зубчатые механизмы часто применяются в коробках скоростей, где передаточное число меняется скачкообразно. Это позволяет, при постоянной угловой скорости на ведущем звене, сообщать выходному звену механизма разные по величине и направлению скорости, и воспроизводить любой ряд передаточных отношений с заданной закономерностью.

Планетарные механизмы

Сложные зубчатые механизмы, в которых ось хотя бы одного колеса подвижна, называются планетарными механизмами.

Планетарные механизмы подразделяются на планетарные редукторы и мультипликаторы, которые обладают одной степенью свободы и обязательно имеют опорное звено, и зубчатые дифференциальные механизмы, число степеней свободы которых два и более, и которые опорного звена обычно не имеют.

К типовым планетарным механизмам относятся:

однорядный планетарный механизм со смешанным зацеплением (механизм Джеймса);

двухрядный планетарный механизм со смешанным зацеплением;

двухрядный планетарный механизм с двумя внешними зацеплениями;

двухрядный планетарный механизм с двумя внутренними зацеплениями.

Элементы планетарного механизма имеют специальные названия:

зубчатое колесо с внешними зубьями, расположенное в центре механизма называется "солнечным";

колесо с внутренними зубьями называют "короной" или "эпициклом";

колеса, оси которых подвижны, называют "сателлитами";

подвижное звено, на котором установлены сателлиты, называют «водило». Это звено принято обозначать не цифрой, а латинской буквой h.

При вращении солнечного колеса сателлиты поворачиваются как рычаг относительно мгновенного центра вращения (опорное колесо неподвижно) и заставляют вращаться водило. При этом планетарные колеса (сателлиты) совершают сложное движение: вращаются вокруг собственной оси (относительно водила) с угловой скоростью и вместе с водилом обкатываются вокруг его оси (переносное движение). Число степеней свободы этого механизма равно единице. Поэтому редуктор имеет постоянное передаточное отношение.

Обычно у реального механизма имеется несколько симметрично расположенных блоков сателлитов . Их вводят с целью уменьшения габаритов механизма, снижения усилия в зацеплении, разгрузки подшипников центральных колес, улучшения уравновешивания водила, хотя механизм в этом случае имеет избыточные связи, т.е. является статически неопределимым. При кинематических расчетах учитывается один сателлит, так как остальные являются пассивными в кинематическом отношении.

Если в рассмотренном механизме освободить от закрепления опорное колесо (корпус редуктора) и сообщить ему вращение, то все центральные колеса станут подвижными и механизм превратится в дифференциальный, так как число степеней свободы его будет равно двум.

Таким образом, дифференциальный механизм – это планетарный механизм с числом степеней свободы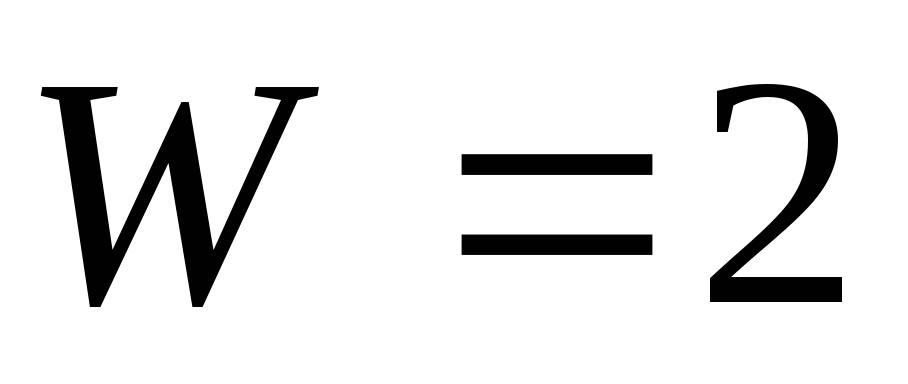

.

Число степеней свободы (подвижности) механизма показывает, скольким звеньям дифференциала необходимо сообщить независимые движения, чтобы получить определенность движения всех остальных звеньев. Здесь в зависимости от направления вращения наружных валов может происходить либо разложение движения (одного ведущего на два ведомых), либо сложение движения. Ведущим считается такой вал, у которого направление скорости вращения и момента совпадают. Следовательно, планетарный редуктор (или мультипликатор), имеющий неподвижное колесо, можно превратить в дифференциал, если освободить неподвижное (опорное) колесо и сообщить ему вращение. Наоборот, любой дифференциал можно превратить в планетарный редуктор, если закрепить одно (при W = 2) или несколько из его центральных колес. Это так называемое свойство обратимости планетарных механизмов, которое позволяет применять одинаковые методы исследования и проектирования для редукторов и для дифференциалов. При этом каждому элементарному дифференциалу будут соответствовать два планетарных редуктора

В таблице приведены структурные схемы типовых планетарных механизмов, а также диапазоны рекомендуемых передаточных отношений и ориентировочные значения КПД при этих передаточных отношениях.

Кинематика зубчатых механизмов

Зубчатая передача, у которой геометрическая ось хотя бы одного из колес подвижна, называется планетарной . Различные планетарные механизмы можно представить в виде трех типов передач.

1. Простые планетарные передачи, обладающие одной степенью подвижности, у которых одно из основных звеньев закреплено неподвижно (рис. 15.7, закреплено звено 3). Такие механизмы служат для последовательной передачи потока мощности.

2. Дифференциальные передачи, обладающие двумя степенями подвижности, у которых все основные звенья подвижны (рис. 15.6). Эти передачи позволяют суммировать два или несколько потоков мощности, поступающих от независимых источников, либо распределять их по независимым потребителям.

3. Замкнутые дифференциальные передачи, получаемые из дифференциальных передач путем замыкания двух основных звеньев (центрального колеса и водила) простой передачей, состоящей из колес 1, 2, 3 (рис. 15.8). Такие передачи позволяют получить большие передаточные отношения при малых габаритах.

Рассмотрим механизм, изображенный на рис. 15.6. Определим число степеней подвижности, если = 4 - число звеньев,и – число кинематических пар V и IV класса.

Определенность в движении звеньев уэтого механизма будет в том случае, если будут заданы законы движения двум звеньям.

Основными звеньями механизмов с подвижными осями являются водило (Н) и соосные с ним колеса (1 и 3). В данном случае все основные звенья подвижные. Оба эти признака (W> 1 и подвижные основные звенья) определяют дифференциальный механизм .

Определим степень подвижности для механизма, изображенного на
рис. 15.7

У этого механизма колесо 3 (основное звено) неподвижно и W= 1. Оба признака определяют планетарный механизм .

Механизмы замкнутых дифференциалов имеют все основные звенья подвижными, но число степеней подвижности равно единице (W= 1). Таким образом, только по совокупности двух признаков механизмы с подвижными осями можно отнести к тому или иному типу.

Формулы 15.5, 15.7 для определения передаточного отношения планетарных и дифференциальных механизмов использовать нельзя, так как сателлит участвует в сложном движении, состоящем из вращения вокруг оси O 2 и вращения вместе с водилом Н вокруг оси О н (см. рис.15.6, 15.7).

Для вывода зависимостей, связывающих угловые скорости механизмов, имеющих подвижные оси, воспользуемся методом обращения движения.

Допустим, что в действительном движении звенья механизма (см.рис.15.6) имеют угловые скорости . Сообщим всем звеньям скорость, равную угловой скорости водила, но противоположно ей направленную, т.е. . В этом случае угловые скорости звеньев будут соответственно равны:

Так как водило Н стало неподвижным (), то мы получили "обращенный механизм" с неподвижными осями. Для этого механизма справедлива зависимость

где –передаточное отношение "обращенного механизма, которое можно определить через число зубьев колес:

В правую часть предыдущей зависимости подставим значение относительных скоростей:

(15.9)

Полученное уравнение называется формулой Виллиса для дифференциальных механизмов . Левая часть, как показано выше, может быть выражена через число зубьев колес. Определенность в решении правой части будет иметь место, когда будут известны скорости двух ведущих звеньев. Установим, какой вид примет формула Виллиса для планетарного механизма, изображенного на рис. 15.7. У этого механизма колесо 3 жестко соединено со стойкой (заторможено), т.е. .

Таким образом, имеем

Откуда (15.10)

Полученную зависимость называют формулой Виллиса для планетарных механизмов, а передаточное отношение – планетарным передаточным отношением .

Как и для дифференциальных механизмов, определяется через число зубьев колес.

В общем случае:

где – передаточное отношение от звена К к звену l (l – соответствует неподвижному центральному колесу).

Достоинством планетарных механизмов является возможность получения больших передаточных отношений при малых габаритах.

Пример 1 . Определить передаточное отношение планетарного механизма (рис. 15.9), если Z 1 = 100, Z 2 = 99, Z 2´ = 100, Z 3´ = 101.Это одноступенчатый планетарный редуктор. Используя формулу (15.10), запишем

Пример 2 . В зубчатой передаче, показанной на рис. 15.10, входное коническое колесо 1 в данный момент имеет угловую скорость = 340 с -1 и постоянное угловое ускорение = 285 с -2 , направленное по движению.

Z 1 = Z 2 = 18; Z 2´ = Z 4´ = 18; Z 3 = Z 5 = 30; Z 3´ = Z 5´ = 22; Z 4 = Z 6 = 70.

Принять средний модуль конического колеса m m = 2 мм, ширину колеса b= 20 мм, плотность ρ = 8000 кг/м, смещение центра масс (точки А, рис.15.11) l = 2 мм.

Определить:

1) передаточное отношение между входным и выходным звеньями и направление вращения;

2) угловую скорость и угловое ускорение выходного звена, их направление показать на схеме передачи;

3) время, в течение которого угловая скорость увеличится в 2 раза;

4) величину и направление силы инерции и момента пары сил инерции звена 1 в начале и в конце найденного в предшествующем пункте промежутка времени, сравнить силу инерции с силой тяжести и показать чертежом направления вращения, ускорения и инерционных нагрузок;

5) общий коэффициент полезного действия передачи.

1. Определить передаточное отношение механизма.

Выделим из механизма ступень с неподвижными осями, состоящую

Деление передач на рядовые и ступенчатые имеет смысл, когда они содержат более двух подвижных звеньев. На рис. 17, а ,б показаны примеры рядовой и ступенчатой передач, соответственно.

Колёса рядовой передачи располагаются в одной плоскости или, иначе, в один ряд, отсюда и происходит название. В ступенчатой передаче каждая пара зацепляющихся колёс располагается в своей плоскости, образует свою ступень. На виде б) :1 ,2 - первая ступень; 3, 4 - вторая.

В рядовой передаче каждое звено содержит только одно зубчатое колесо. Номер звена и номер колеса совпадают. В ступенчатой передаче колёса 2 и3 располагаются на одной ступени (одном валу), поэтому иногда они обозначаются номером вала, на котором они располагаются, и различаются по индексу, например 2′, 2′′ или 2а, 2б. Номер звена не проставляется, так как содержится в обозначениях колёс.

Рядовая и ступенчатая передачи образуют класс передач с неподвижными осями колёс . Для любой такой передачи передаточное отношение от первого звена к последнему,n -му,равно произведению промежуточных передаточных отношений. Это правило выражается формулой

u1,n = u1,2u2,3... un-1,n , (12)

где индексы указывают номера звеньев. Для доказательства справедливости формулы представим каждое u в виде отношения скоростей:

ω1 = ω1ω2 Lωn −1 .

ωn ω2ω3ωn

После сокращений уравнение обращается в тождество, что и доказывает справедливость формулы (12). Формула справедлива для любой последовательной цепи механизмов. При этом uij (здесь и далее запятую опускаем) есть передаточное отношение отдельного механизма.

Применим формулу (12) к передачам, изображённым выше. Для рядовой передачи

u =u u u			z	2		−	z	3	−	z	4	=−	z	4	.
	=	−
	z	z	z
14 12 23	34				2			3		z
				1								1

Для ступенчатой передачи

			z2 ′		z3			z2 ′z3
u =u u =	−		−	=	.
z	z
13 12 23						z z
		1		2 ′′			1 2 ′′

Результаты показывают, что передаточное отношение рядовой передачи зависит от чисел зубьев только крайних колёс. Ступенчатая передача не обладает таким свойством. Знак «минус» в передаточном отношении u14 показывает, что колёса1 ,4 вращаются в разные стороны.

11. Дифференциальные и планетарные передачи. Формула Виллиса.

К типовым планетарным механизмам относятся:

· однорядный планетарный механизм со смешанным зацеплением (механизм Джеймса);

· двухрядный планетарный механизм со смешанным зацеплением;

· двухрядный планетарный механизм с двумя внешними зацеплениями;

· двухрядный планетарный механизм с двумя внутренними зацеплениями.

Элементы планетарного механизма имеют специальные названия:

· зубчатое колесо с внешними зубьями, расположенное в центре механизма называется "солнечным";

· колесо с внутренними зубьями называют "короной" или "эпициклом";

· колеса, оси которых подвижны, называют "сателлитами";

· подвижное звено, на котором установлены сателлиты, называют «водило». Это звено принято обозначать не цифрой, а латинской буквой h.

Таким образом, дифференциальный механизм – это планетарный механизм с числом степеней свободы .

Типовые планетарные механизмы

№	Структурная схема механизма	Uред	КПД
		3....10	0.97....0.99
		7....16	0.96....0.98
		25....30	0.9....0.3
		30....300	0.9....0.3

Формула Виллиса

Формула Виллиса выводится на основании основной теоремы зацепления и устанавливает соотношение между угловыми скоростями зубчатых колес в планетарном механизме. Рассмотрим простейший планетарный механизм с одним внешним и одним внутренним зацеплением. Всему механизму сообщается угловая скорость равная по величине и противоположна по направлению угловой скорости водила, при этом водило остановится, а опорное колесо начнет поворачиваться. Таким образом, планетарный механизм превратится в механизм с неподвижными осями, состоящий из нескольких последовательно соединенных зубчатых колес. Такой механизм носит название обращенного механизма.

Угловые скорости звеньев в каждом из рассматриваемых движений приведены в таблице

В движении звеньев относительно водила угловые скорости звеньев равны угловым скоростям в движении относительно стойки минус угловая скорость водила. Если в движении относительно стойки ось сателлита подвижна, то в движении относительно водила оси обоих зубчатых колес неподвижны. Поэтому к движению относительно водила можно применить основную теорему зацепления.

Передаточное отношение обращенного механизма , окончательно передаточное отношение планетарного редуктора может быть определено по формуле Виллиса:

Передаточное отношение планетарного редуктора от любого колеса к водилу равно единице минус передаточное отношение обращенного механизма от этого колеса к опорному.

При пересопряжении зубьев следующий зуб второго колеса должен попасть в следующую впадину первого, т.е. шаги на находящихся в зацеплении колес должны быть одинаковыми:

Таким образом, для одной пары колес прямо пропорционально отношению и обратно пропорционально отношению чисел зубьев колес, составляющих пару:

Знак передаточного отношения показывает направление вращения колеса на выходе по отношению к направлению вращения на входе:

(+) – направления вращения на входе и на выходе совпадают. Для пары колес направление вращения совпадает при внутреннем зацеплении (рисунок 35б);
(–) – колеса вращаются в противоположные стороны. Это происходит при внешнем зацеплении (рисунок 35а).

На рисунке 35 дана фронтальная проекция передач, а также их условное изображение на кинематических схемах при виде сбоку (или в разрезе).

Многоступенчатая передача

Для увеличения кинематического эффекта несколько зубчатых пар могут последовательно соединяться в единый . Такой механизм называется многоступенчатым зубчатым механизмом или многоступенчатой передачей . Схема одного из таких механизмов приведена на рисунке 36.

Рисунок 36

Запишем передаточные отношения для каждой пары колес данного механизма:

Из схемы видно, что колеса 2 и 3 находятся на одном валу и вращаются с одной угловой скоростью (ω 2 = ω 3 ), аналогично ω 4 = ω 5 . Поэтому в приведенном выше уравнении эти члены сократились.

Таким образом, общее передаточное отношение многоступенчатого механизма равно произведению частных передаточных отношений ступеней, из которых состоит данный механизм:

В этой формуле “m” – число передач внешнего зацепления (если число передач внешнего зацепления четное, то знак "+", т.е. колеса на входе и на выходе вращаются в одну сторону; если нечетное, то знак "–". Количество передач внутреннего зацепления не учитывается, т.к. внутреннее зацепление не изменяет направление вращения).

В приведенном примере m=2 (пары Z 1* Z 2 и Z 3* Z 4 ; пара Z 5* Z 6 – пара внутреннего зацепления) и, таким образом, колеса "1" и "6" вращаются в одну сторону.

Планетарные и дифференциальные механизмы

В практике применяются зубчатые механизмы, имеющие колеса с подвижными геометрическими осями (сателлиты ). Такие механизмы называются планетарными (если имеют одну ) или дифференциальными (если степень свободы равна двум).

Планетарные и дифференциальные механизмы позволяют получить более высокий кинематический эффект, более высокий , более удобную компоновку. Дифференциальные механизмы позволяют также раскладывать одно движение на два или складывать два движения в одно.

Рисунок 37

На рисунке 37 приведен пример дифференциального (рисунок 37 а) и планетарного механизмов (рисунок 37 б). В этих механизмах колесо "2" имеет подвижную геометрическую ось – это и есть сателлит.

Неподвижная геометрическая ось, вокруг которой движется ось сателлита, называется центральной осью . Колеса, геометрические оси которых совпадают с центральной, также называются центральными (на рисунке 37 колеса "1" и "3" – иногда такие колеса называют солнечными). , соединяющее ось сателлитов с центральной осью, называется водилом (водило обычно обозначается "H").

Записываем уравнение передаточного отношения между центральными колесами этого многоступенчатого механизма (для того, чтобы отличить передаточное отношение механизма с остановленным водилом от первоначально заданного, в верхнем индексе ставят обозначение водила H. Для данного примера читается – передаточное отношение от первого к третьему при остановленном водиле):

Формулу такого типа, полученную на основе метода обращения движения, называют формулой Виллиса. В данном конкретном механизме (рисунок 38) имеется еще одна особенность – колесо 2 входит последовательно в два зацепления (с первым и третьим колесами), являясь ведомым для первого колеса и ведущим – для второго.

Полученная формула является универсальной для обоих механизмов, изображенных на рисунке 37. Дифференциальный механизм, изображенный на рисунке 37а, имеет две степени свободы, а поэтому для определенности движения надо задать законы движения двум звеньям. При этом возможны следующие варианты:

заданы ω 1 и ω 3 ; из записанной формулы определяется ω H (вариант, изображенный на рисунке 37 а);
заданы ω 1 и ω H ; из записанной формулы определяется ω 3 ;
заданы ω H и ω 3 ; из записанной формулы определяется ω 1 .

Так как звеньям можно задавать любые законы движения, то, как частный случай, одному из центральных колес зададим угловую скорость, равную нулю. Например, в рассматриваемом механизме зададим ω 3 =0 , другим словами, затормозим третье колесо. Таким приемом отнимается одна из двух степеней свободы, и механизм из дифференциального превращается в планетарный (рисунок 37 б).

Таким образом, планетарный механизм это частный случай дифференциального, когда одно из центральных колес неподвижно (заторможено).

Поэтому решаются эти механизмы совершенно одинаково, по одним и тем же уравнениям, только в планетарном механизме для неподвижного колеса в уравнение подставляется значение угловой скорости, равное нулю. Для изображенного на рисунке 37б планетарного механизма: